うっかりE問題を見てしまい1週間うんうん唸り続ける羽目になったけどようやくなんとなくわかったのでメモ。公式解説のほかいろいろ見た。問題名でググって出てくるとこは大体目を通しましたよと。もはやどれを参考にできたかも覚えておらぬ。
解説の流れ
https://img.atcoder.jp/diverta2019/editorial.pdf
の番号がついた
個のマスが左から右に向かって並んでいる。 マス
には整数
が書かれている。 すぬけ君ははじめに好きな整数
を任意に選んだのち、駒をマス
に置く。 その後、以下のルールで駒を動かす。
- 現在駒が置かれているマスより、番号が大きいマスにしか動かせない
- 現在駒が置かれているマスに
が書かれているなら、
が書かれているマスに駒を移動させなくてはならない
- 現在駒が置かれているマスに
が書かれているなら、
が書かれているマスに駒を移動させなくてはならない
最終的に駒がマス
に置かれているように駒を動かす方法は何通りあるか?
与えられた数列を、各要素を
とおく。
の累積xorの数列を
、各要素を
とおく。
与えられた数列を分割して作成した数列を、
数列
の要素を
とおく。下図みたいな感じ。
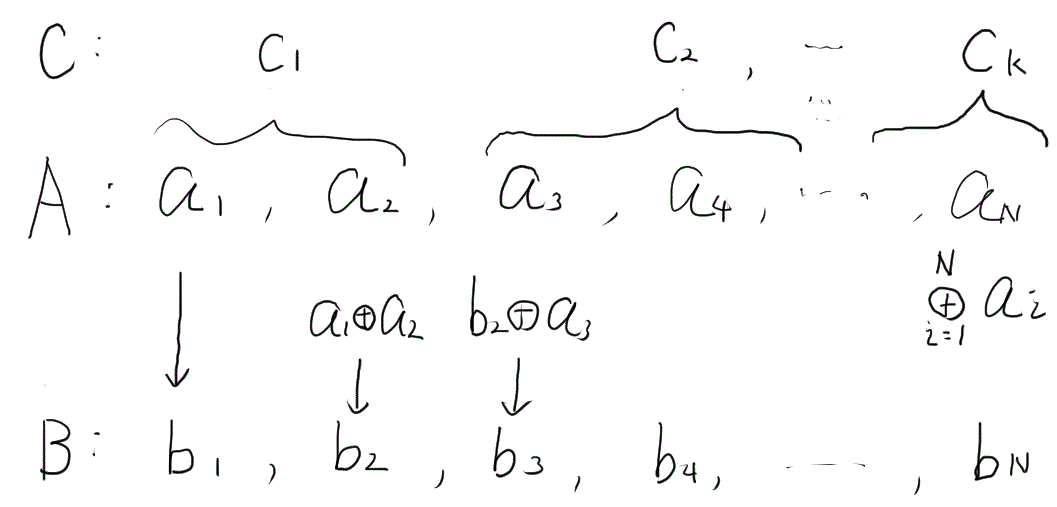
ある値で
たちの美しさが全て等しくなるとする。このとき、
の要素に対してxorを取ると
。
に対して累積xorを取ると
と、
が交互に並ぶ形になる。
の要素から
と
に注目し、交互に並ぶように選べば美しさが等しい分割となる。

簡単のため
が
でない場合を考えます。このときは
が一意に定まります。
だから
。
なら
と
が一意に定まる。
0/Xの遷移に加え、前の値の代わりに自分の値を使えるということだろう(あまり理解してない)

の場合は特殊ですが、容易に計算可能です。
値がの
の数が
個とすれば
(単に仕切りをどこにいれるかという話)。
を
と
以外の数を取り除いたのち、ランレングス圧縮を行った数列における
の出現回数は
における
の出現回数で抑えられることが重要です。
は
に隣接していることになるので、圧縮すればせいぜい
の出現数
なる
に関する遷移をうまく遷移をまとめると
うまくまとめる・・・

ここで詰んだので他の解説やらを探すと次の方のコードおよび解説のおかげでなんとなくわかりました。ありがとうございます。
D:k個の区間の選択を、x[0]=0<x[1]<x[2]<...<x[k-1]<x[k]=Nとなるようなx[1],...,x[k-1]の選択と同一視する。Sを累積xorとして、条件は0=S[x[0]]=S[x[2]]=S[x[4]]=...、S[x[1]]=S[x[3]]=S[x[5]]=...と書ける。
— selpoAC (@selpoAC) 2019年5月11日
Submission #5380934 - diverta 2019 Programming Contest
自分の理解は次のようになります。あってるかどうかは知らぬ。
]から
]への影響は途中にある
の個数による。

漸化式は
※最初の1は初手でを選ぶ場合
上手く計算(の累積和、区間の
の個数を記録しておく)すれば
。それぞれの
の出現回数の総数は
なので全体として
となる。
次のようにして区間の
の数を出せるようにしておけば使いまわせる。
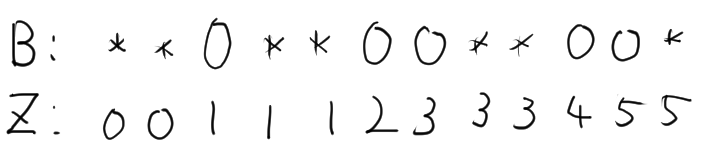
所感
難しい・・・とても難しい・・・。考え方がわかってたとしても時間内に終わる気しねえ・・・。
