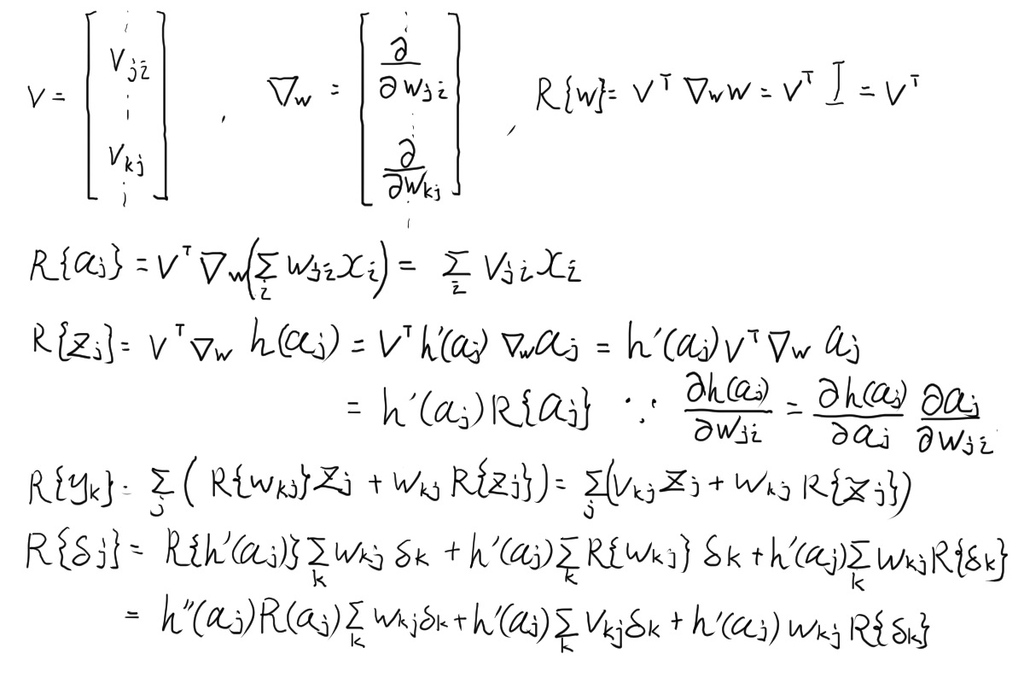PRML 5.4.3～5.4.6 - trsing’s diary

5.4.3　ヘッセ行列の逆行列

外積による近似を用いた場合にヘッセ行列の逆行列の近似を逐次的に計算する手順

初期値 $H_{0}=\alpha I$ を選ぶ
$b_{L+1}\equiv \nabla_{w}a_{L+1}$ を算出する
$H_{L+1}$ を算出する(5.89)
$L+1=N$ となるまで2,3を繰り返す

※ $H+\alpha I$ の逆行列を見つけることになる

導出
外積を(5.86)と表記すると、 $$ H_{N+1}=\sum_{n=1}^{N}b_{n}b_{n}^{T}+b_{N+1}b_{N+1}^{T}=H_{N}+b_{N+1}b_{N+1}^{T} $$ これに対して行列の恒等式(5.88)を利用すると(5.89)。

5.4.4　有限幅の差分による近似

1階微分のように(5.69)有限幅の差分による近似と同じ方法で導出すると(5.90) 残留誤差は $O(\epsilon^{2})$ 、計算量は $O(W^{3})$ 。

誤差関数の1階微分に中心差分を応用すると(5.91)。計算量は $O(W^{2})$ 。

(5.90)について $$ \frac{\partial }{\partial w_{ji}}\frac{\partial E}{\partial w_{lk}} =\frac{1}{2\epsilon}(E(w_{lk}+\epsilon)-E(w_{lk}-\epsilon))\\= \frac{1}{2\epsilon}\left( \frac{E(w_{ji}+\epsilon,w_{lk}+\epsilon)-E(w_{ji}+\epsilon,w_{lk}-\epsilon)}{2\epsilon}- \frac{E(w_{ji}-\epsilon,w_{lk}+\epsilon)-E(w_{ji}-\epsilon,w_{lk}-\epsilon)}{2\epsilon} \right)\\= \frac{1}{4\epsilon^{2}}\left( E(w_{ji}+\epsilon,w_{lk}+\epsilon)-E(w_{ji}+\epsilon,w_{lk}-\epsilon)- E(w_{ji}-\epsilon,w_{lk}+\epsilon)+E(w_{ji}-\epsilon,w_{lk}-\epsilon) \right) $$

5.4.5　ヘッセ行列の厳密な評価

逆伝播のテクニックの拡張を利用して任意のフィードフォワード構造を持つネットワークのヘッセ行列を厳密に求めることができる。ネットワークの出力の関数として表すことができる微分可能な誤差関数、微分可能な活性化関数を持つネットワーク、にも適応できる。計算量は $O(W^{2})$ 。

(5.55),(5.56)に注意して計算する f:id:trsing:20190203155551j:plain

(5.93)について f:id:trsing:20190203155603j:plain

(5.94)について f:id:trsing:20190203155612j:plain

(5.95)について f:id:trsing:20190203155624j:plain

5.4.6　ヘッセ行列の積の高速な計算

必要となるのはヘッセ行列自体ではなく、 $H$ とあるベクトル $v$ の積。 $v^{T}H$ を計算量 $O(W)$ で評価できるアプローチを示す。

方法
$\nabla E$ を評価するための標準的な順伝播と逆伝播の方程式を書き下し、これに微分演算子 $v^{T}\nabla$ を作用させると $v^{T}H$ を評価するための方程式の集合を得ることができる。

例) 2層ネットワーク、線形出力ユニット、二乗和誤差関数の場合。

順伝播方程式に微分演算子を作用させる
順伝播方程式は(5.98),(5.99),(5.100)。これに $v^{T}\nabla$ (以下 $\mathcal{R}\{\}$ と表記)を作用させると (5.101),(5.102),(5.103)を得る。
逆伝播方程式に微分演算子を作用させる
逆伝播の式は(5.104),(5.105)。これに $\mathcal{R}\{\}$ を作用させると (5.106),(5.107)を得る。
$v^{T}H$ の要素を得る
誤差の1階微分は(5.108),(5.109)。これに $\mathcal{R}\{\}$ を作用させると $v^{T}H$ の要素による式 (5.108),(5.109)を得る。